Lo spaziotempo di Minkowski

La relatività ristretta ha fatto decadere il postulato del tempo assoluto. Come conseguenza dato un evento in un sistema di riferimento, sono da indicare le specifiche coordinate spaziali e temporali. Il tempo non è più una variabile assoluta, indipendente nel suo scorrere dal sistema di riferimento.

La lunghezza come tempo

Il nuovo contesto rende plausibile considerare le quattro variabili allo stesso livello. Se consideriamo un velocità fissa possiamo addirittura utilizzate il tempo come indicatore di una distanza (es. Londra dista due giorni a cavallo, la distanza tra il Sole e la stella più vicina è di circa 4 anni luce) equiparandolo a una coordinata spaziale.

Possiamo utilizzare a tale scopo la velocità c il cui valore è assoluto e invariante. Moltiplicando il tempo per una costante abbiamo sempre un'indicazione di tempo, ma espressa in una unità di misura diversa. Facciamo la stessa operazione quando per esempio esprimiamo un intervallo temporale di 2h in minuti: (60×2)m. Al contempo se la costante moltiplicatrice è una velocità abbiamo anche una valorizzazione spaziale essendo vt=x. Indichiamo con la lettera T questa rappresentazione del tempo.

T = ct

Utilizziamo la nuova definizione di tempo nella rappresentazione della velocità relativa tra due sistemi inerziali.

x x v
— = —— = — = β
T ct c

Essendo il risultato di un rapporto tra velocità il risultato è un numero puro adimensionale. Il suo valore spazia nell' intervallo [0, 1] con valore unitario nel caso di espressione della velocità della luce nel vuoto.

Le nuove variabili permettono di semplificare ulteriormente le trasformazioni di Lorentz.

x = γ(x' + vt')

x = γ(x' + (v/c)ct')

x = γ(x' + βT')

t = γ(t' + (v/c²)x')

tc = γ(ct' + (v/c)x')

T = γ(T' + βx')

┌
│ x = γ(x' + βT')
│
│
│ T = γ(T' + βx')
└

Abbiamo ottenuto due formule coincidenti nella forma. Applicando il tempo nella prima e lo spazio nella seconda non se ne perde la validità.

La quadriposizione e la quadridistanza

In un contesto relativistico un sistema di riferimento deve essere costituito da tre coordinate spaziali e una temporale. La sua notazione si espande di una dimensione rispetto ai sistemi classici. Il modo alternativo possiamo esprimere un punto nella quadridimensione come:

xⁱ = [cτ, x, y, z] = [x⁰, x¹, x², x³]

Come sappiamo le proprietà di uno spazio sono definite dalla sua metrica. Nello spazio euclideo a tre dimensioni la metrica è definita dalla funzione della distanza pitagorica.

ds² = dx² + dy² + dz²

Applichiamo le trasformazioni di Galileo alla funzione per vedere come si comportano le distanze se osservate in sistemi inerziali differenti.

ds² = (dx' + vdt)² + dy'² + dz'²

Data la rilevazione della distanza in un preciso istante che comporta dt=0 dimostriamo che la distanza è invariante al cambio di coordinate.

ds² = dx² + dy² + dz² = dx'² + dy'² + dz'²

Non conosciamo le proprietà dello spaziotempo di Minkowski, ma possiamo tentare di ricavare una proprietà metrica simile. Adottiamo allora la stessa formula della distanza, ma ponendovi anche la coordinata temporale:

ds² = dT² + dx² + dy² + dz²

ds² = γ²(dT' + βx')² + γ²(dx' + βdT')² + y'² + z'²

ds² = γ²dT'² + γ²β²x'² + 2γ²T'dx' + γ²dx'² + γ²β²dT'² + 2γ²dT'dx' + y'² + z'²

Se avessimo posto il segno negativo a dτ o a dx (e con esso per coerenza a dy e dz) avremmo ottenuto la semplificazione cercata.

ds² = dT² − dx² − dy² − dz²

ds² = γ²(dT' + βx')² − γ²(dx' + βdT')² − y'² − z'²

ds² = γ²dT'² + γ²β²x'² + 2γ²dτ'dx' − γ²dx'² − γ²β²dT'² − 2γ²dT'dx' − y'² − z'²

ds² = γ²dT'²(1 − β²) − γ²x'²(1 − β²) − y'² − z'²

ds² = dT'² − dx'² − dy'² − dz'²

Abbiamo semplificato sapendo che per loro definizione γ²(1 − β²)=1.

Nei passaggi appena svolti abbiamo trovato e dimostrato che una metrica con spazio e tempo a segni opposti garantisce che l'intervallo spaziotemporale tra due eventi è invariante per le trasformazioni di Lorentz.

xⁱ = [x⁰, −x¹, −x², −x³]

L'opposizione di segno tra tempo e spazio si traduce in una metrica dello spaziotempo definita dalla matrice η.

┌ ┐

│ 1 0 0 0 │

│ 0 −1 0 0 │

η = │ 0 0 −1 0 │

│ 0 0 0 −1 │

└ ┘

Confrontando la metrica con le leggi di trasformazione di Lorentz troviamo una verifica nel segno opposto che spazio e tempo hanno all'interno di queste.

Il tempo proprio

Dalla definizione di intervallo temporale e dall'avere dimostrato la sua invarianza al cambio di coordinate nei sistemi inerziali possiamo estrarre una formula per il tempo. Scriviamo l'intervallo percorso da una particella rilevandolo da un un sistema inerziale relativo R e da un sistema R' solidale alla particella. Semplifichiamo le formulazioni raccogliendo le coordinate spaziali in una unica.

ds'² = c²dt'² − dx'² = c²dT² − dx² = ds²

In R' sistema solidale con la particella, il moto di questa non è percepito, quindi dx'=0.

dt' = ds/c

La quantità dt', il tempo misurato nel sistema comovente all'evento osservato è detto tempo proprio e indicato con la lettera greca tau: dτ.

Se suddividiamo la traiettoria di una particella in tratti infinitesimi, ciascuno definibile in un sistema inerziale, ciascuno con un tempo proprio, possiamo integrare i tempi in un tempo proprio complessivo della particella anche se il suo moto complessivo non è inerziale.

L'intervallo spaziotemporale

L'avere coinvolto il tempo come coordinata di un punto impone di sostituire il concetto di punto nello spazio con quello di evento nello spaziotempo. Parimenti il termine distanza che ricorda uno scostamento meramente spaziale è sostituibile dal termine intervallo.

Aggiungiamo che l'avere posto dei termini negativi nel calcolo dell'intervallo comporta che contrariamente a quanto accade nello spazio euclideo per la distanza, nello spaziotempo si possono avere intervalli negativi. Questo è uno dei motivi che porta all'utilizzo della sua versione al quadrato cosa che evita l'inconveniente di un possibile argomento di radice negativo.

Deduciamo quindi che dati due eventi E₁, E₂ possiamo classificare intervalli positivi, nulli e negativi.

ds²(E₁, E₂) > 0 ⟷ |cdτ| > |dx| intervallo di tipo tempo

ds²(E₁, E₂) = 0 ⟷ |cdτ| = |dx| intervallo di tipo luce

ds²(E₁, E₂) < 0 ⟷ |cdτ| < |dx| intervallo di tipo spazio

Una distanza positiva tra due eventi indica una prevalenza del tempo sullo spazio, il tempo trascorso tra il loro succedersi è maggiore della distanza che li separa. Il contrario nel caso di una distanza negativa.

Significativo è capire anche la dinamica di una distanza, quanto varia la distanza spaziale al variare di quella temporale, in pratica qual è la velocità u di moto nello spazio del secondo evento rispetto al primo. Calcoliamola.

c²dτ² − dx² > 0

c²dτ² > dx²

c > dx/dτ

c > u

Nel caso di un intervallo di tipo tempo la distanza spaziale tra due eventi si evolve a una velocità inferiore a quella della luce. Tra i due eventi è possibile una relazione di causa-effetto e una comunicazione con interazioni viaggianti a velocità intermedia tra v e c.

c²dτ² − dx² = 0

c = u

L'intervallo luce indica invece una velocità di allontanamento pari a quella della luce. Solo la luce e poche altre interazioni (gravitazionali, forze nucleari, ...) possono essere così descritte.

c²dτ² − dx² < 0

c < u

Nel caso di un intervallo di tipo spazio la distanza spaziale tra due eventi si evolve a una velocità superiore a quella della luce. Tra i due eventi non è possibile ci sia alcuna una relazione o comunicazione.

La quadrivelocità

La velocità nello spaziotempo differisce da quella euclidea in quanto deve riguardare non la sola derivata temporale dello spostamento spaziale dx bensì la derivata dell'intervallo ds=d(ct−x). Se la velocità viene osservata da un altro sistema inerziale dobbiamo esprimere l'argomento della derivata attraverso le trasformazioni di Lorentz. Per quanto sopra deriviamo ds² per il tempo proprio del sistema inerziale di ds.

ds d(γct' + γx'v/c) d(γx' + γct'v/c)
( —— )² = ( ———————————————— )² − ( ———————————————— )²
dτ dτ dτ

ds
( —— )² = (γc)² − (γv)²
dτ

ds c² − v²
( —— )² = ————————————
dτ (c² − v²)/c²

U² = U∙U = c² > 0

U = c

Abbiamo denominato con U la quadrivelocità. Essendo U un vettore, il suo quadrato è definito da un prodotto vettoriale, la cui soluzione è norma quadra del quadrivettore. Questa è una costante positiva dello spaziotempo. Si è qui dimostrato che c, quale limite di velocità delle interazioni, è tale in quanto corrisponde a un vincolo dello spaziotempo. Il valore di c non è il limite, ma l'unica velocità a cui ci si può muovere nello spaziotempo.

La velocità di spostamento di qualunque fenomeno nello spaziotempo è invariante. Questo significa avere un modulo costante. L'unica libertà è nella direzione, intesa come spostamento più o meno sbilanciato verso lo spazio o il tempo. Una particella ferma in un sistema di riferimento impegna tutta la velocità nello spostamento temporale. Si comprende come un comportamento opposto, il muoversi a velocità luminare, significhi non muoversi nel tempo. Si può da qui dedurre che per un fotone il tempo non scorre, non si avrà mai un suo decadimento.

La quadrivelocità può essere scomposta nella componente tempo e spazio.

U² = (U⁰)² − (Uⁱ)² i = 1,2,3

U⁰ = cdt/dτ

Uⁱ = dxⁱ/dτ

La quadrivelocità misurata da un sistema esterno, quindi rapportata al tempo relativo si trasforma applicando la relazione dτ=dt/γ.

U⁰ = γcdt/dt = γc

Uⁱ = γdxⁱ/dt = γuⁱ

La quadriaccelerazione

Adattiamo la formulazione classica allo spaziotempo e definiamo la quadriaccelerazione di una particella, misurata rispetto al tempo proprio del sistema in cui avviene lo spostamento ds.

A = dU/dτ

Anche per la quadriaccelerazione possiamo scomporre il suo quadrivettore in un vettore temporale e in un trivettore spaziale.

A = A⁰ - Aⁱ

A = d(γc)/dτ - d(γuⁱ)/dτ

A = 0 - d(γuⁱ)/dτ < 0

Osserviamo come, essendo l'accelerazione temporale nulla, la quadriaccelerazione è un quadrivettore di tipo spazio, con norma negativa.

Possiamo esprimere la quadriaccelerazione anche in funzione della velocità e dell'accelerazione spaziale.

A⁰ = (dU⁰/dt)(dt/dτ) = (d(γc)/dt)γ = (dγ/dt)cγ

Aⁱ = (dUⁱ/dt)(dt/dτ) = (d(γuⁱ)/dt)γ = ((dγ/dt)uⁱ + γ(duⁱ/dt))γ = ((dγ/dt)uⁱ + γaⁱ)γ

In entrambe le equazioni compare la derivata temporale di γ della quale non conosciamo l'espressione. Iniziamo a calcolare con la regola della derivata composta la più semplice derivata di dγ per du per poi applicarvi dt

dγ/du = d(1 - u²/c²)^-1/2/du

dγ/du = -1/2(1 - u²/c²)^-3/2(-2u/c²)

dγ = γ³(udu/c²)

dγ/dt = (γ³/c²)(u∙a)

Applichiamo la derivata temporale di γ ai componenti della quadriaccelerazione.

A⁰ = (γ⁴/c)(u∙a)

Aⁱ = (γ⁴/c²)(u∙a)uⁱ + γ²aⁱ

Dall'assunzione di una velocità costante nello spaziotempo ricaviamo che il modulo della velocità rimane costante. Ne consegue che l'accelerazione non può interessare il modulo, ma solo la direzione. Geometricamente significa che la quadriaccelerazione è un vettore ortogonale alla quadrivelocità che ne orienta la direzione, verso un maggiore o minore scorrimento nello spazio o nel tempo. In termini matematici implica che il prodotto scalare tra i due quadrivettori deve essere nullo, essendo questa la condizione di ortogonalità.

A∙U = 0

Lo spaziotempo

Diamo una rappresentazione geometrica dello spaziotempo in uno spazio cartesiano. Poniamo il piano orizzontale xy come rappresentazione di uno spazio bidimensionale, mentre la retta ordinata (verticale) indica la coordinata temporale.
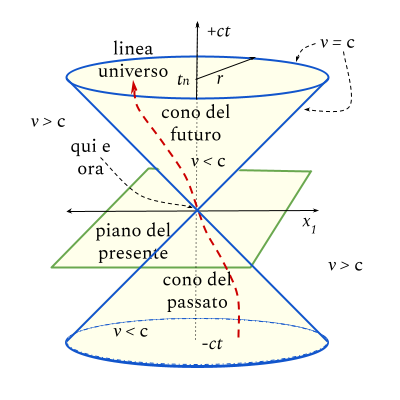
Eventi posti sullo stesso piano orizzontale si trovano in luoghi diversi, ma sono simultanei tra loro, mentre eventi posti sullo stesso asse verticale si susseguono nello stesso luogo in tempi diversi. Una successione di eventi o una ripetizione di uno stesso evento diviene una successione di punti che vanno a costituire una linea detta linea universo.

Le linee universo si muovono dal basso verso l'alto, seguendo la linea del tempo. Linee universo verticali indicano il succedersi o il ripetersi di un evento nel tempo sempre in un dato luogo dello spazio. Linee universo orizzontali non sono invece possibili in quanto rappresenterebbero uno spostamento nello spazio senza avanzamento nel tempo.

Il diagramma è costruito su un evento posto all'origine degli assi cartesiani. Esso rappresenta contemporaneamente un luogo dello spazio e l'istante del presente nel tempo. Da questo punto ci si può allontanare nello spazio tempo a velocità comprese nell'intervallo [-1, 1]. Nel diagramma sono rappresentate nei loro valori estremi, da rette orizzontali (-1) o verticali (-1) passanti per l'origine. Una velocità 0 è invece rappresentata da una retta avente inclinazione di 45°. Quest'ultimo caso definisce una successione di intervalli che si discostano l'uno dal successivo a una velocità c. Queste diagonali rappresentano il confine dello spazio reale.

Nello spaziotempo reale gli eventi si succedono a velocità inferiori a c. Questo implica che le linee universo passanti per l'origine non possono avere inclinazione inferiore a 45°. Rimangono racchiuse in un cono che si allarga nel futuro e nel passato. Il cono futuro è costituito dalla sovrapposizione di dischi orizzontali che rappresentano dato un istante del tempo tutti i luoghi che partendo dall'origine di potrebbero raggiungere con velocità comprese tra (0, c). Il cono del passato rappresenta i punti dai quali è possibile arrivare all'origine. Esternamente al cono si trovano i punti con i quali l'origine non può avere contatti.

La rappresentazione iperbolica

Osserviamo come mentre la formula della distanza nello spazio euclideo ricorda l'equazione del cerchio, la formula dell'intervallo spaziotemporale con il suo segno negativo ricorda quella iperbolica.

y² − x² = 1

Possiamo quindi ricondurre la formula della distanza in notazione goniometrica.

T² − x² = s²

(ct)² − (vt)² = s²

(c)² − (v)² = s/t²

(c)² − (v)² = c²

c² − v² = 1

Nel secondo termine dell'equazione abbiamo trovato la quadrivelocità che sappiamo avere valore costante pari a c. Abbiamo poi posto per semplificazione c=1. Questo ci permette di sostituire i termini con gli equivalenti iperbolici.

cosh²(θ) − sinh²(θ) = 1

c = cosh(θ)

v = sinh(θ)

Possiamo ricavare di conseguenza:

v sinh(θ)
β = — = ——————— = tanh(θ)
c cosh(θ)

1 1 1
γ = —————————— = ———————————————————————— = ———————————————— = cosh(θ)
(1 − β²)^1/2 cosh²(θ) − sinh²(θ) 1
( ——————————————————— )^1/2 ( ——————————— )^1/2
cosh²(θ) cosh²(θ)

γβ = sinh(θ)

Sostituiamo i termini delle leggi di trasformazione di Lorentz con i loro corrispondenti iperbolici

x' = γx − γβT

T' = γT − γβx

x' = − T sinh(θ) + x cosh(θ)

T' = T cosh(θ) − x sinh(θ)

Questa nuova formulazione ci ricorda le leggi euclidee di trasformazione delle coordinate a seguito di una rotazione degli assi.

x' = − y sin(θ) + x cos(θ)

y' = y cos(θ) + x sin(θ)

Le trasformazioni di Lorentz sono quindi assimilabili a trasformazioni per rotazione del piano iperbolico di un angolo θ detto rapidità.

La differenza tra le due rotazioni sta nei segni. Nella geometria euclidea la rotazione degli assi è concorde nella direzione, asimmetrica rispetto alla bisettrice del primo quadrante. Nello spazio iperbolico invece le trasformazioni di Lorentz sono simmetriche, cosa che si riflette in un comportamento di rotazione convergente verso la bisettrice del primo quadrante. 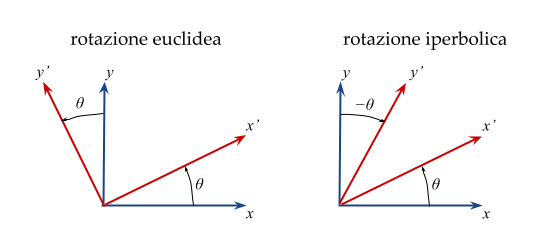Nello spaziotempo se osservate da un sistema esterno, gli assi di un dato sistema di riferimento sono visti convergere verso la bisettrice tanto quanto più è elevata la velocità relativa tra i due sistemi. A velocità prossime a quella della luce nel vuoto i due assi tendono a coincidere sulla bisettrice. In caso di velocità relativa dei sistemi negativa, il grafico viene rappresentato in modo speculare all'asse T sul secondo quadrante del piano cartesiano.

Possiamo dimostrare questo comportamento considerando due punti: A(0,1) posto sull'asse x e B(1,0) posto sull'asse T del sistema solidale R. Le coordinate dei punti viste da un sistema inerziale non solidale differiscono per le trasformazioni di Lorentz. Applichiamo quindi le trasformazioni alle coordinate dei punti espresse nel sistema R e otteniamo le coordinate come appaiono in R'.

A(0, 1) = (γ0 + γβ1, γ1 + γβ0) = A'(γβ, γ)

B(1, 0) = (γ1 + γβ0, γ0 + γβ1) = B'(γ, γβ)

Calcoliamo l'inclinazione della retta passante per A' e l'origine O(0,0). Questa coincide con l'asse x'

T' − T γβ − 0
m_P = —————— = ——————— = β
x' − x γ − 0

Lo stesso facciamo per l'inclinazione della retta passante per B' e l'origine O(0,0), coincidente con l'asse T'

T' − T γ − 0
m_Q = —————— = ——————— = 1/β
x' − x γβ − 0

Lo stesso risultato è ottenibile con il calcolo trigonometrico.

sin(θ)
m_P = —————— = tan(θ) = β
cos(θ)

cos(θ)
m_Q = —————— = 1/tan(θ) = 1/β
sin(θ)

Dati i coefficienti angolari gli assi di riferimento del sistema R' rispondono in coordinate di R alle equazioni:

x' ⟶ T = βx

T' ⟶ x = βT ⟶ T = x/β

Il coefficiente β ha valore tra 0 e 1. Applicato all'asse x', consente un'inclinazione compresa tra l'orizzontale e i 45°. Per T'i avendo come coefficiente 1/β i valori ammissibili sono inversi, tra infinito e 1, ossia tra un orientamento verticale e un'inclinazione a 45°. Il valore β=1 è ottenuto solo se v=c.

L'angolo non ortogonale tra gli assi del sistema R' comporta che a un versore (vettore unitario) in x corrisponde a un versore in x' di diversa lunghezza. Dall'esempio precedente abbiamo come versore di x il tratto OA=1. Troviamo il valore del corrispondente versore di x', il tratto OA', misurato nelle coordinate di R.

A'(γβ, γ)

OA'² = γ² + γ²β² = γ²(1 + β²)

(1 + β²)^1/2
OA' = ——————————— > 1
(1 − β²)^1/2

Il tratto OA' è stato qui definito in coordinate di R ossia usando come unità di misura il versore OA. Nel sistema comovente R', in unità di misura di R' misura invece 1 in quanto OA' è un versore del sistema R'.

Un qualunque tratto DE in R, parallelo all'asse x in coordinate di R misura s=DE/OA. In modo analogo un tratto D'E' in R', parallelo all'asse x' in coordinate di R' misura s'=D'E'/OA'. 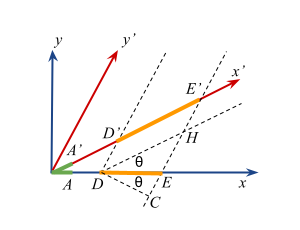Osservando la figura vediamo come i tratti DE e D'E' possono essere calcolati come ipotenuse dei triangoli retti DCE e DCH, essendo in quest'ultimo caso D'E'=DH. Avendo detti triangoli base comune possiamo metterli in relazione .

DEcos(θ) = D'E'cos(2θ)

DE cos(2θ)
———— = ———————
D'E' cos(θ)

Avendo trovato che tan(θ)=β scriviamo i termini trigonometrici in funzione di β

cos²(θ) 1 1
cos²(θ) = ————————————————— = —————————— = ———————
cos²(θ) + sin²(θ) 1 + tan²(θ) 1 + β²

1 − β²
cos(2θ) = cos²(θ) − sin²(θ) = cos²(θ)(1 − tan²(θ)) = ———————
1 + β²

Sostituiamo questi termini nell'uguaglianza.

DE cos(2θ) 1 − β²
———— = ——————— = —————— (1 + β²)^1/2
D'E' cos(θ) 1 + β²

I due segmenti sono qui espressi seguendo il disegno geometrico, quindi esprimendoli in una stessa unità di misura. Ricordiamo che in R l'unità di misura è il versore OA, mentre in OA' è il versore OA'. Riportiamo i due segmenti in termini delle loro unità di misura.

s DE OA' 1 − β² (1 + β²)^1/2(1 + β²)^1/2
—— = —— ———— = ———————————————————————————
s' OA D'E' 1 + β² (1 − β²)^1/2

s = s'(1 − β²)^1/2

γs = s'

Abbiamo così dimostrato la contrazione della distanza. In modo analogo possiamo lavorare sugli assi T-T' per dimostrare la dilatazione dei tempi. Essendo questi assi ortogonali (in modo euclideo e iperbolico) a x-x' la formulazione nella dimensione temporale ha forma inversa.

γ/t = 1/t'

γt' = t

Il boost di Lorentz

Le trasformazioni di coordinate regolate dalle leggi di Lorentz possono essere raccolte in una matrice quadrata a cui applicare per moltiplicazione un vettore di coordinate x per ottenere un secondo vettore espresso in coordinate y. Chiamiamo boost l'azione di trasformazione delle coordinate di Lorentz: Λ(v). Il boost in quanto diretta derivazione del fattore di Lorentz ha come unica variabile indipendente la velocità v.

Λ(v)X = Y

┌ ┐ ┌ ┐ ┌ ┐
│ γ −γβ 0 0 │ │ x⁰ │ │ y⁰ │
│ │ │ │ │ │
│ −γβ γ 0 0 │ │ x¹ │ = │ y¹ │
│ │ │ │ │ │
│ 0 0 0 0 │ │ x² │ │ y² │
│ │ │ │ │ │
│ 0 0 0 0 │ │ x³ │ │ y³ │
└ ┘ └ ┘ └ ┘